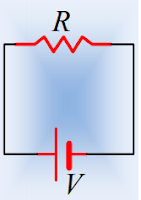
Διαθέτουμε έναν αντιστάτη με αντίσταση R=10Ω την οποία
συνδέουμε με μια πηγή σταθερής τάσης V=5Ω, όπως στο σχήμα.
i) Να βρεθεί η ένταση του ρεύματος που διαρρέει
τον αντιστάτη.
ii)
Ένας μαθητής Α θέλοντας να μετρήσει την παραπάνω ένταση του ρεύματος, χρησιμοποιεί
ένα αμπερόμετρο με εσωτερική αντίσταση rΑ =2Ω. Να σχεδιάστε το
κύκλωμα που θα χρησιμοποιήσει και να βρείτε την ένδειξη του αμπερομέτρου.
iii)
Ένας δεύτερος μαθητής Β, μη γνωρίζοντας την τιμή της αντίστασης R, χρησιμοποιεί
το παραπάνω αμπερόμετρο και ένα βολτόμετρο με εσωτερική αντίσταση rv=100Ω,
δημιουργώντας το παρακάτω κύκλωμα.
α) Ποιες θα είναι οι ενδείξεις των οργάνων;
β) Ποια η πειραματική τιμή της αντίστασης Rπ
που υπολογίζει;
iv)
Ένας τρίτος μαθητής Γ, υποστηρίζει ότι θα ήταν ακριβέστερη η μέτρηση, αν
χρησιμοποιούσε τα όργανα σε σύνδεση, όπως στο διπλανό κύκλωμα. Είναι σωστή η
εκδοχή αυτή;
v)
Τέλος ένας μαθητής Δ χρησιμοποιεί ιδανικά
όργανα, αμπερόμετρο και βολτόμετρο, στην ίδια διάταξη με τον Β.
α) Ποιες είναι οι εσωτερικές αντιστάσεις των
οργάνων;
β) Ποιες είναι οι ενδείξεις των οργάνων και ποια
είναι η πειραματική αντίσταση Rπ,Γ την οποία υπολογίζει;
ή
 |