Η ενέργεια διατηρείται, αλλά και υποβαθμίζεται.

Σύμφωνα με τον 1^ο Θερμοδυναμικό νόμο, η ενέργεια διατηρείται. Η μεταβολή στην εσωτερική ενέργεια ενός συστήματος, μπορεί να προκύψει αν το σύστημα ανταλλάξει ενέργεια με δύο ισοδύναμους τρόπους. Είτε μέσω έργου, είτε μέσω θερμότητας.

Δηλαδή το έργο και η θερμότητα εμφανίζονται σαν δυο ισοδύναμοι τρόποι μεταφοράς ενέργειας.

Θα μπορούσε λοιπόν κάποιος να πει, ότι είτε έχω αποθηκευμένη μια ενέργεια 1000J σε μια ποσότητα νερού, με τη μορφή της δυναμικής ενέργειας (έχοντας το νερό αυτό σε κάποιο ύψος) είτε με τη μορφή της εσωτερικής (θερμικής) ενέργειας (έχοντας αυξήσει τη θερμοκρασία της ίδιας ποσότητας νερού) το αποτέλεσμα είναι το ίδιο.

Εδώ όμως έρχεται ο 2^ος Θερμοδυναμικός νόμος για να μας πει, ότι τα πράγματα δεν είναι έτσι. Και αυτό γιατί:

Ενώ μπορούμε να πάρουμε έργο W=1000J, αν αφήσουμε το νερό να πέσει από την πρώτη δεξαμενή, δεν μπορούμε να κατασκευάσουμε μια θερμική μηχανή, μέσω της οποίας να αντλήσουμε θερμότητα 1000J από την δεύτερη δεξαμενή και να πάρουμε έργο 1000J.

Η ενέργεια που είναι αποθηκευμένη σαν θερμική ενέργεια είναι χειρότερης ποιότητας από την αντίστοιχη μηχανική ενέργεια…

Έτσι συνηθίζουμε να λέμε ότι η θερμότητα είναι κατώτερης ποιότητας ενέργεια, σε σύγκριση με το έργο.

Αλλά ένα ποσό θερμότητας έχει πάντα την ίδια αξία; Η απάντηση είναι όχι.

«Σε όσο μικρότερη θερμοκρασία βρίσκεται ένα ποσό θερμότητας τόσο υποβαθμισμένο είναι».

Ας το δούμε με μια εφαρμογή.

Άσκηση:

Πρόκειται να εκμεταλλευτούμε ένα ποσό θερμότητας Q_h=1000J, το οποίο θα αντλήσουμε από μια δεξαμενή Α, χρησιμοποιώντας μια θερμική μηχανή η οποία θα χρησιμοποιεί σαν δεξαμενή χαμηλής θερμοκρασίας την ατμόσφαιρα σε θερμοκρασία 27°C. Πόσο είναι το μέγιστο ποσό έργου που μπορούμε να πάρουμε στην περίπτωση που η θερμοκρασία .... συνέχεια.

Απόδοση κύκλου, που έχει και μια αδιαβατική μεταβολή.

Ένα αέριο εκτελεί την παρακάτω αντιστρεπτή κυκλική μεταβολή. Από την κατάσταση Α σε πίεση p_Α=32∙10⁵Ν/m² και όγκο V_Α=1L, με ισοβαρή θέρμανση φτάνει σε κατάσταση Β με όγκο V_Β=8L. Μετά ψύχεται ισόχωρα μέχρι κατάσταση Γ, από όπου με αδιαβατική συμπίεση επανέρχεται στην αρχική του κατάσταση Α.

i)  Να παραστήσετε τη μεταβολή σε άξονες p-V.

ii) Πόσο έργο παράγει το αέριο σε κάθε κυκλική μεταβολή;

iii) Υπολογίστε την απόδοση μιας ... συνέχεια.

Άλλο ένα διαγώνισμα Φυσικής Β Γενικής

Ένα σημειακό φορτίο q=10μC αφήνεται στο σημείο Α ενός ηλεκτρικού πεδίου, οπότε μετά από λίγο φτάνει στο σημείο Β έχοντας κινητική ενέργεια 0,1J.

i)   Πόσο είναι το έργο της δύναμης του πεδίου από το Α στο Β;

ii)  Να βρείτε τη διαφορά δυναμικού V_Α-V_Β.

iii) Αν η δυναμική ενέργεια του σωματιδίου στη θέση Β είναι 0,2J, να βρείτε την δυναμική του ενέργεια στο σημείο Α.

iv)  Να σχεδιάστε την ένταση του ηλεκτρικού πεδίου στο σημείο Α.

Δείτε όλο το διαγώνισμα από εδώ.

Εφαρμογή του 1ου Θερμοδυναμικού νόμου σε κυκλική μεταβολή.

Μια ποσότητα αερίου διαγράφει την κυκλική μεταβολή του παρακάτω σχήματος.

Αν p_Α=2p_Γ=2∙10⁵Ν/m², V_Α=10L, ενώ η προέκταση της ΒΓ περνά από την αρχή των αξόνων. Δίνεται ακόμη ότι κατά τη μεταβολή ΑΒ το αέριο απορροφά θερμότητα 6000J.

i)  Να βρεθεί ο όγκος στην κατάσταση Β.

ii)  Να υπολογισθεί το έργο, η θερμότητα και η ..... 

συνέχεια..

1ος Θερμοδυναμικός νόμος και μη αντιστρεπτή μεταβολή.

Μια ποσότητα αερίου πηγαίνει μη αντιστρεπτά από την κατάσταση ισορροπίας Α στην κατάσταση Β του παρακάτω διαγράμματος, απορροφώντας θερμότητα 1000J.

i)   Πόσο μετεβλήθη η εσωτερική ενέργεια του αερίου;

ii)  Πόσο έργο παρήχθη;

iii) Αν η μετάβαση από την αρχική κατάσταση Α πήγαινε στην κατάσταση Β, μέσω της διαδρομής A→Γ→Β:

α)  Πόσο έργο θα παρήγαγε;

β) Πόση θερμότητα..... 

 συνέχεια.

Διαγώνισμα Φυσικής Γεν. Παιδείας. Στατικός Ηλεκτρισμός.

1)  Στο σημείο Ο του διπλανού σχήματος, υπάρχει ακλόνητο σημειακό φορτίο +Q. Στο σημείο Α, σ’ απόσταση r αφήνουμε ελεύθερο ένα σωματίδιο Σ με φορτίο +q₁.

i)  Να σχεδιάστε την δύναμη που ασκείται πάνω του. Το μέτρο της δίνεται από την εξίσωση:

F= ……………….

ii)  Σχεδιάστε επίσης το διάνυσμα της έντασης του πεδίου (που οφείλεται στο φορτίο Q) στο σημείο Α. Το μέτρο της έντασης δίνεται από την εξίσωση:

Ε=…………….

iii) Μετά από λίγο το Σ φτάνει στο σημείο Β, όπου (ΟΑ)=(ΑΒ). «Τότε δέχεται δύναμη με μέτρο ίσο με το μισό του αντίστοιχου μέτρου της δύναμης στο Α». Να εξηγείστε αν η παραπάνω πρόταση είναι σωστή ή λανθασμένη.

2)   Δίνονται δύο αντίθετα φορτία +q, -q, όπως στο σχήμα. Να σχεδιάστε τις δυναμικές γραμμές του ηλεκτρικού πεδίου των δύο φορτίων. Να σχεδιάστε επίσης την ένταση του πεδίου στο σημείο Α, αφού έχετε προνοήσει να περάσει μια δυναμική γραμμή από το Α.

3)  Ένα φορτισμένο σωματίδιο με φορτίο q= - 10μC αφήνεται στο σημείο Α μιας δυναμικής γραμμής, όπου V_Α= 1000V και μετά από λίγο περνά από ένα σημείο  (Β ή Γ) έχοντας κινητική ενέργεια Κ=0,01J.

i)    Υπολογίστε την δυναμική ενέργεια του σωματιδίου στο σημείο Α.

ii)   Από ποιο  σημείο πέρασε το σωματίδιο, το Β ή το Γ και γιατί;

iii)  Πόσο έργο παράγεται από την δύναμη του πεδίου κατά την διάρκεια της παραπάνω μετακίνησης του σωματιδίου;

iv) Να υπολογίσετε το δυναμικό στο σημείο αυτό (Β ή Γ).

4)  Στα άκρα ενός ευθυγράμμου τμήματος ΑΒ ...

     συνέχεια...

Ωριαίο διαγώνισμα στα αέρια (και εσωτερική ενέργεια).

1)     Μια ποσότητα ιδανικού αερίου διαγράφει τις μεταβολές του παρακάτω σχήματος, όπου Τ_Α=Τ_Δ.

i)      Πώς ονομάζονται οι μεταβολές αυτές;

ii)    Σε ποιους νόμους υπακούουν οι μεταβολές ΑΒ και ΒΓ; (Να δοθεί το όνομα και η μαθηματική εξίσωση που περιγράφει κάθε μεταβολή).

iii)  Να σχεδιάστε ποιοτικά τις μεταβολές αυτές στους διπλανούς άξονες V-Τ.

2)     Δύο δοχεία Α και Β του ίδιου όγκου, περιέχουν το Α 4g Η₂ και το Β 4g Ο₂ στην ίδια θερμοκρασία.

i)      Τίνος αερίου τα μόρια έχουν μεγαλύτερη μέση κινητική ενέργεια;

ii)    Ποιο αέριο έχει μεγαλύτερη εσωτερική ενέργεια;

iii)  Ποιου αερίου τα μόρια έχουν μεγαλύτερη ενεργό ταχύτητα;

iv)  Σε ποιο δοχείο επικρατεί μεγαλύτερη πίεση;

Δίνονται οι γραμμομοριακές μάζες Μ_Η2=2∙10^-3kg/mοℓ και Μ_Ο2=32∙10^-3kg/mοℓ.

Να δικαιολογήστε εν συντομία τις απαντήσεις σας.

3)     Μια ποσότητα Ηe βρίσκεται σε κατακόρυφο δοχείο που κλείνεται με έμβολο μάζας 2kg και εμβαδού 10cm², απέχοντας κατά h₁=5cm από την βάση του. Η θερμοκρασία του αερίου είναι 300Κ.

i)      Πόση είναι η πίεση του αερίου και π.....

συνέχεια..

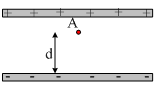
Επιτάχυνση φορτισμένου σωματιδίου από Ηλεκτρικό πεδίο.

Ένα σωματίδιο μάζας m=0,01mg και φορτίου q₁=1nC, αφήνεται στο σημείο Α, ενός ομογενούς ηλεκτρικού πεδίου έντασης Ε=3∙10⁷Ν/C, οπότε μετά από λίγο κτυπά στην αρνητική πλάκα αφού διανύσει απόσταση d=1,5cm.

i) Σε πόσο χρόνο και με ποια ταχύτητα το σωματίδιο φτάνει στην αρνητική πλάκα;

ii)  Να παραστήσετε γραφικά την ταχύτητα του σωματιδίου σε συνάρτηση με το χρόνο.

Το ίδιο σωματίδιο αφήνεται στο σημείο Α, σε απόσταση r=4cm από ένα σταθερό σημειακό φορτίο Q=2μC.
   iii) Ποια είναι η μέγιστη ταχύτητα που αποκτά το σωματίδιο;
   iv) Κάνετε επίσης ένα ποιοτικό διάγραμμα της ταχύτητας του σωματιδίου σε συνάρτηση με το χρόνο.

Οι βαρυτικές δυνάμεις θεωρούνται αμελητέες και k=9∙10⁹Ν∙m²/C².

Απάντηση:

Ένταση και δυναμικές γραμμές ενός ηλεκτροστατικού πεδίου. Ένα Τεστ.

1)  Να σχεδιάστε το διάνυσμα της έντασης του ηλεκτρικού πεδίου που δημιουργεί το σημειακό φορτίο Q στα σημεία Α και Β. Αν το μέτρο της έντασης στο σημείο Β είναι ίσο με 3∙10⁵Ν/C, πόσο είναι το αντίστοιχο μέτρο της έντασης στο Α, αν (ΟΑ)=(ΑΒ) ;

2) Στα σημεία Α και Β (μακριά το ένα από το άλλο) φέρνουμε δύο κατ’ απόλυτο τιμή ίσα φορτία +q και –q. Στο σχήμα έχουν σχεδιαστεί οι δυνάμεις ίσου μέτρου, που δέχονται από το ηλεκτρικό πεδίο, κάποιων άλλων φορτίων. 

Να σχεδιάστε την ένταση του ηλεκτρικού πεδίου στα σημεία Α και Β, στο ίδιο σχήμα. Σε ποιο σημείο στο Α ή στο Β το πεδίο είναι ισχυρότερο; Να δικαιολογήσετε την απάντησή σας.

3)  Στα σημεία Α και Β του διπλανού σχήματος έχουμε τοποθετήσει δύο σημειακά φορτία q₁ και q₂ Στο σχήμα βλέπετε την ένταση του πεδίου στο σημείο Ρ, που οφείλεται στο φορτίο q₂ το μέτρο της οποίας είναι Ε₂=10⁷Ν/C.

i)  Ποιο το πρόσημο ... συνέχεια

Ένταση Ηλεκτρικού πεδίου. Ένα Τεστ.

Στις κορυφές Α και Γ ενός τετραγώνου έχουμε τοποθετήσει δύο σημειακά φορτία κατ’ απόλυτη τιμή ίσα |q₁|=|q₂|=2μC. Στο σχήμα βλέπετε την ένταση του πεδίου στο κέντρο Ο του τετραγώνου, που οφείλεται στο φορτίο q₁ η οποία έχει μέτρο Ε₁=18∙10⁷ Ν/C.

i)   Ποιο είναι το πρόσημο του φορτίου q₁ και πόση είναι η απόσταση (ΑΟ);

ii)  Αν η συνολική ένταση στο σημείο Ο κατευθύνεται προς την κορυφή Γ, να υπολογίστε το μέτρο της ....

συνέχεια..

Θέρμανση ανοικτού μπουκαλιού.

Σε ένα μπουκάλι με ανοικτό στόμιο περιέχεται αέρας σε θερμοκρασία 27°C. Θερμαίνουμε το αέριο μέχρι να ανέβει η θερμοκρασία του στους 127°C.

i)    Η παραπάνω θέρμανση είναι η γνωστή μας ισοβαρής θέρμανση;

ii)  Τι ποσοστό του αρχικού αριθμού μορίων .....

  συνέχεια

Ένταση Ηλεκτρικού πεδίου.

Στο σχήμα έχει σχεδιαστεί η ένταση του ηλεκτρικού πεδίου, στο σημείο Ο, που  οφείλεται στο σημειακό ηλεκτρικό φορτίο q₁ που βρίσκεται στο σημείο Α, η οποία έχει μέτρο Ε=100Ν/C.

i)   Τι πρόσημο έχει το φορτίο  q₁;

ii)  Στο σημείο Β φέρνουμε ένα σημειακό φορτίο q₂=+1μC. Βρείτε το φορτίο που πρέπει να φέρουμε στο σημείο Γ, αν (ΟΒ)=(ΟΓ), ώστε να μη μεταβληθεί η ένταση του πεδίου στην αρχή Ο των αξόνων.

iii)  Τοποθετούμε στο σημείο Δ ένα

συνέχεια...

Μεταβολές αερίων.

Στο παρακάτω σχήμα δίνονται οι μεταβολές μιας ποσότητας ιδανικού αερίου, όπου η ΑΒ πραγματοποιείται υπό σταθερή θερμοκρασία.

Πώς ονομάζονται οι μεταβολές αυτές;
Η ΑΒ είναι μια ισόθερμη εκτόνωση. Γιατί εκτόνωση; Τι σημαίνει η λέξη αυτή;
Εκτόνωση σημαίνει αύξηση του όγκου, με ταυτόχρονη μείωση της πίεσης. Αυτά τα δύο πρέπει να συμβαίνουν μαζί. Διαφορετικά δεν πρέπει να χρησιμοποιείται ο όρος.
Η μεταβολή ΒΓ, είναι μια ισοβαρής. Τι ισοβαρής; Σύμφωνα με μια διαδεδομένη λογική μπορεί να ονομασθεί ισοβαρής συμπίεση, μιας και ο όγκος μειώνεται. Ναι, αλλά αφού δεν αυξάνεται η πίεση, τότε πώς μπορεί να είναι συν-πίεση; Ο όρος είναι λανθασμένος. Το αέριο ψύχεται υπό σταθερή πίεση και γι’ αυτό μειώνεται ο όγκος του. Ο σωστός λοιπόν όρος που περιγράφει τη μεταβολή είναι: Ισοβαρής ψύξη.
Η μεταβολή ΓΑ; Και εδώ χρησιμοποιείται ο όρος ισόχωρη συμπίεση, όπου και πάλι είναι λανθασμένος. Συμπίεση σημαίνει να μετακινήσουμε ένα έμβολο, μειώνοντας τον όγκο και αυξάνοντας την πίεση. Εδώ έχουμε ένα δοχείο με σταθερό όγκο που απλά θερμαίνεται. Η μεταβολή πρέπει να αποκαλείται: Ισόχωρη θέρμανση.


Εφαρμογή:
Ένα αέριο εκτελεί την κυκλική μεταβολή ...
Συνέχεια ....

Απόδοση θερμικής μηχανής.

Ιδανικό μονοατομικό αέριο εκτελεί τις παρακάτω  μεταβολές: ΑΒ τυχαία γραμμική εκτόνωση  με εξίσωση Ρ=4Ρο-(Ρο/Vo)∙V από το σημείο Α(3Po,Vo) στο σημείο Β(Ρο,3Vo), BΓ ισοβαρής ψύξη μέχρι τον αρχικό όγκο Vo και τέλος ΓΑ ισόχωρη θέρμανση. 

           Συνέχεια.... 

Ένας απολογισμός και μια πορεία.

Κατ’ αρχήν καλή σχολική χρονιά σε όλους. Να είμαστε καλά και με κέφι να παλέψουμε για μια ακόμη φορά. Και ότι πετύχουμε….

Συμπληρώνονται σχεδόν δύο χρόνια από τη στιγμή που δημιούργησα την Ιστοσελίδα «Εκπαιδευτικό Υλικό Φυσικής-Χημείας Λυκείου» και ταυτόχρονα άρχισα να γράφω κάποιες ασκήσεις στο blogspot. Δημοσίευσα κάποιο υλικό που είχα, ενώ οι Ασκήσεις απευθυνόταν στους μαθητές που αναζητούσαν κάποια βοήθεια. Έτσι ξεκίνησε η ιστορία…

Δεν πίστευα και δεν περίμενα ότι πολλοί συνάδελφοι θα ενδιαφερόντουσαν και θα παρακολουθούσαν την προσπάθεια αυτή. Πολύ δε περισσότερο, δεν περίμενα μια μεγάλη προσφορά θεμάτων προς δημοσίευση απόσυναδέλφους, αλλά και την ανάπτυξη ενός ζωντανού διαλόγου μεταξύ συναδέλφων, πάνω στα θέματα που έβγαιναν κάθε τόσο μέσω του Blog, κυρίως της Γ΄ Λυκείου.

Αν κάποιος παρακολουθούσε τις αναρτήσεις μετά τα Χριστούγεννα, θα διαπίστωσε ότι πάνω από το 80% αφορούσαν υλικό, προσφορά κάποιου συνάδελφου. Ο οποίος μου έστελνε την άσκηση και εγώ την δημοσίευα. Έτσι στην πράξη το υλικό δεν ήταν πλέον του Μάργαρη, αλλά μιας μεγάλης ομάδας συναδέλφων.

Ο διάλογος ήταν ανοικτός και ελεύθερα κάποιος μπορούσε να κρίνει και να σχολιάζει, ακόμη και ανώνυμα τα πράγματα, με τεχνικούς όμως τρόπους καθόλου εύκολους, μέσω των σχολίων.

Η στάση των περισσοτέρων συναδέλφων που συμμετείχαν στο διάλογο, ήταν έντιμη και υπεύθυνη, χωρίς να απουσιάζουν όμως και περιπτώσεις που αν μη τι άλλο πρόσβαλλαν τον συνομιλητή…

Και τώρα τι κάνουμε; Πώς συνεχίζουμε; Πώς εκμεταλλευόμαστε τις νέες δυνατότητες που μας προσφέρει η εξέλιξη της τεχνολογίας; Πώς λαμβάνουμε υπόψη τη διαμορφωμένη κατάσταση και πώς διορθώνουμε τα πράγματα, ώστε να ελαχιστοποιηθούν τα αρνητικά φαινόμενα που παρουσιάστηκαν, ενώ αντίθετα να προωθηθούν ιδέες και να αναδειχθούν νέες προοπτικές;

Μετά από έντονο προβληματισμό, κατέληξα ότι τη νέα χρονιά θα έπρεπε να κινηθούμε στοχεύοντας στα εξής:

1) Να ανοίξουμε το σύστημα, ώστε να περάσουμε πραγματικά, από ένα Blog του Μάργαρη, σε ένα κοινωνικό δίκτυο συνεργαζομένων Καθηγητών, που γράφουν ισότιμα, ανταλλάσσουν υλικό και ιδέες, αντιπαρατίθενται αν χρειαστεί, υπεύθυνα και ελεύθερα, έχοντας και την ευθύνη των λεγομένων τους.

2) Να βελτιωθεί ο τρόπος σχολιασμού των πραγμάτων, αφού μέσω των σχολίων τα πράγματα δεν ήταν καθόλου εύκολα, αφού κάποιος δε μπορούσε να γράψει ούτε μια εξίσωση, πολύ δε περισσότερο, να απαντήσει αναλυτικά, δίνοντας την δική του εκδοχή ενός φαινομένου.

3) Να αποκλεισθεί, στο μέτρο του δυνατού, η δυνατότητα καθενός κακοήθους, ο οποίος κρυπτόμενος πίσω από την ανωνυμία, μπορούσε να υποβαθμίζει το διάλογο και να προβοκάρει…

Έτσι δημιούργησα το δίκτυο «Υλικό Φυσικής-Χημείας», στο οποίο θα μεταφέρω την αρχική Ιστοσελίδα αφενός και αφετέρου συνέδεσα με επτά (7) νέα blogs στο Blogspot, ένα ανά μάθημα και τάξη, ενώ το 7^ο θα περιέχει θέματα μόνο για καθηγητές, αφού η εμπειρία έδειξε ότι εκεί υπάρχει έντονο ενδιαφέρον από συναδέλφους και καλό θα ήταν τα θέματα αυτά να μην τα έβλεπαν μαθητές, μαζί με τα θέματα που απευθυνόταν στους ίδιους.

Στο εξής λοιπόν σταματούν να ενημερώνονται τα υπάρχοντα blogs (για όσο χρόνο χρειαστεί θα υπάρχουν διπλοεγγραφές) και το νέο υλικό θα αναρτάται εκεί. Εκεί, αλλά και πρώτα όμως, στο Ιστολόγιο του δικτύου, όπου θα είναι ευκολότερος ο σχολιασμός των συναδέλφων.

Καλείται κάθε συνάδελφος ο οποίος θεωρεί ότι μπορεί να συμβάλει στην προσπάθεια αυτή, να γραφτεί σαν μέλος του δικτύου και όλοι μαζί να δημιουργήσουμε μια συλλογή θεμάτων, χρήσιμη για κάθε διδάσκοντα, αλλά και για κάθε μαθητή. Καλούνται ιδιαίτερα οι συνάδελφοι Χημικοί να στηρίξουν την προσπάθεια, αφού νομίζω ότι εκεί υπάρχει μικρότερη προσφορά.

Θα αποστείλω προσωπική πρόσκληση για εγγραφή, μόνο στους συναδέλφους οι οποίοι τις προηγούμενες χρονιές μου είχαν αποστείλει υλικό για δημοσίευση, αλλά το δίκτυο είναι ανοικτό για όλους, είτε θέλουν να γράψουν κάτι δικό τους, είτε απλά να σχολιάσουν ή να θέσουν κάποιο ερώτημα.

Υπάρχει βέβαια και η δυνατότητα κάποιος να παρακολουθεί μόνο κάποιο blog και να σχολιάσει σε αυτό κάποιο θέμα, όμως ο σχολιασμός θα είναι και εκεί επώνυμος, αφού δεν δίνεται πλέον η δυνατότητα ανώνυμου σχολιασμού.

Σας περιμένω λοιπόν στη διεύθυνση «Υλικό Φυσικής-Χημείας» συνεχίζοντας την προσπάθεια από εκεί..

Φόρτιση πυκνωτή και Aυτεπαγωγή.

Έστω και μετά από ημέρες, καλοκαίρι γαρ, ας συνεχίσουμε την συζήτηση (εκμεταλλευόμενοι μια μικρή διακοπή στις ..διακοπές μας) γύρω από το αν «χάνουμε» και πόση ενέργεια κατά την φόρτιση ενός πυκνωτή. Κατ’ αρχήν να ξεκαθαρίσουμε τι εννοούμε όταν λέμε ότι «φορτίζουμε ένα πυκνωτή από σταθερή τάση V»; Για μένα αυτό σημαίνει ότι: Αποκαθίσταται ΣΤΑΘΕΡΗ διαφορά δυναμικού μεταξύ των οπλισμών ίση με V και ότι ο πυκνωτής αποκτά ΣΤΑΘΕΡΟ φορτίο q=CV. Εάν αυτό γίνεται αποδεκτό, μπορούμε να προχωρήσουμε. Αν με τον όρο αυτό εννοούμε κάτι άλλο, ας το ξεκαθαρίσουμε από πριν.

Ας προσπαθήσουμε λοιπόν να δώσουμε μια ολοκληρωμένη απάντηση, με χρήση όσο γίνεται, λιγότερων Μαθηματικών*¹. Μπορεί η προσπάθεια να είναι λιγότερο «επιστημονική» αλλά ίσως είναι περισσότερο διαφωτιστική από την πλευρά της Φυσικής που μας ενδιαφέρει. Στόχος της μελέτης αυτής είναι να αποδειχθεί ότι το 50% της παρεχόμενης από την πηγή ενέργειας, δεν καταλήγει τελικά στον πυκνωτή.

Να ξεκινήσουμε με μια άσκηση, από τα γνωστά…

Άσκηση:

Ένα σώμα ηρεμεί στο σημείο Γ, πάνω σε λείο οριζόντιο επίπεδο δεμένο στο άκρο ιδανικού ελατηρίου, σταθεράς k. Σε μια στιγμή t=0 δέχεται την επίδραση μιας σταθερής οριζόντιας δύναμης F, όπως στο σχήμα.

i) Να αποδειχθεί ότι το σώμα θα εκτελέσει α.α.τ. και να βρεθεί η εξίσωσης της απομάκρυνσης σε συνάρτηση με το χρόνο, θεωρώντας την προς τα δεξιά κατεύθυνση θετική.

ii) Να γίνει το διάγραμμα της απόστασης s του σώματος από την αρχική θέση ηρεμίας του σε συνάρτηση με το χρόνο.

iii) Αν η ταλάντωση του σώματος είναι φθίνουσα, εξαιτίας μικρών αποσβέσεων, να γίνει ένα ποιοτικό διάγραμμα της απόστασης s σε συνάρτηση με το χρόνο. Τι ποσοστό της ενέργειας που μετεφέρθη στο σύστημα, μέσω του έργου της δύναμης F, αποθηκεύεται τελικά στο ελατήριο;

Συνέχεια…

Δυναμικό αγωγού αλλά και ενέργειες.

Ας εξετάσουμε με αφορμή την ανάρτηση: Ενέργεια πυκνωτή πόση είναι η χωρητικότητα ενός κυκλικού δίσκου ακτίνας R, αλλά επίσης γιατί να χρησιμοποιούμε πυκνωτή και όχι έναν αγωγό και τέλος ας δούμε αν μπορούμε να υπολογίσουμε την ενέργεια ενός πυκνωτή βρίσκοντας την δυναμική ενέργεια αλληλεπίδρασης των φορτίων του.

Βρήκαμε ότι πάνω στην κάθετη στο κέντρο του δίσκου και σε απόσταση ℓ το δυναμικό δίνεται από την εξίσωση:

Έτσι για ℓ=0 βρίσκουμε το δυναμικό του δίσκου:

Συνεπώς η χωρητικότητα ενός τέτοιου αγωγού είναι:

Η σχέση (α) θα μπορούσε να γραφεί:

Συμπέρασμα η χωρητικότητα ενός μεμονωμένου αγωγού είναι ίση με την χωρητικότητα ενός επίπεδου πυκνωτή που η απόσταση των οπλισμών του είναι ίση με το μισό της ακτίνας του. Αν λάβουμε υπόψη ότι σε ένα πραγματικό πυκνωτή η απόσταση μεταξύ των οπλισμών του είναι πάρα πολύ μικρότερη από R/2, βλέπουμε ότι ο πυκνωτής έχει μεγαλύτερη χωρητικότητα από έναν μόνο αγωγό.

Αν λοιπόν φορτίσουμε έναν τέτοιο δίσκο, με τον τρόπο που φαίνεται στο σχήμα και λάβουμε υπόψη μας την απόδειξη της ανάρτησης Φόρτιση πυκνωτή. Τι γίνεται με τις ενέργειες; Υπολογίζουμε την ενέργεια του αγωγού:

Ας επιστρέψουμε τώρα σε έναν επίπεδο πυκνωτή, με οπλισμούς δύο κυκλικούς δίσκους. Πόση είναι η ενέργειά του;

Όπως έχει ήδη αναφερθεί θα μπορούσαμε να γράψουμε:

U= U_(+q)+U_(-q)+U_(+q,-q)

Όπου U_(+q) είναι η δυναμική ενέργεια αλληλεπίδρασης των θετικών φορτίων μεταξύ τους, U_(-q) η αντίστοιχη λόγω αλληλεπίδρασης των αρνητικών φορτίων μεταξύ τους και U_(+q,-q) η δυναμική ενέργεια αλληλεπίδρασης κάθε θετικού φορτίου του οπλισμού Α με τα αρνητικά φορτία του οπλισμού Β.

Αλλά η σχέση (β) δίνει την δυναμική ενέργεια αλληλεπίδρασης των φορτίων του θετικού οπλισμού, ομοίως και η ενέργεια της αλληλεπίδρασης των αρνητικών φορτίων του άλλου οπλισμού είναι επίσης U_(-q)=q²/4πε_οR, ενώ η ενέργεια αλληλεπίδρασης των θετικών με τα αρνητικά την έχουμε υπολογίσει:

Άρα η συνολική δυναμική ενέργεια αλληλεπίδρασης των φορτίων και των δύο οπλισμών του πυκνωτή είναι ίση:

Θεωρώντας λοιπόν ότι R²+ℓ²≈R² παίρνουμε:

Βλέπουμε πράγματι ότι η ενέργεια που παρέχει η πηγή φόρτισης, αποθηκεύεται στα φορτία του πυκνωτή, με την μορφή της δυναμικής ενέργειας αλληλεπίδρασης, όλων των φορτίων μεταξύ τους.

Ενέργεια πυκνωτή. Ένα σχόλιο και μια απάντηση.

Σχόλια:

Για την απόδειξη της σχέσης 3 θεώρησες ένα σημείο (το Β) στην κάθετη στον κύκλο και στο κέντρο του.
Αν αντί για αυτό διαλέγαμε ένα άλλο σημείο, π.χ. το Β' στην ίδια απόσταση από τον κύκλο, αλλά σε άλλη θέση "πάνω" από τον κύκλο, το αποτέλεσμα του υπολογισμού θα ήταν διαφορετικό. Αλλά πάλι θα έπρεπε ολόκληρος ο οπλισμός Β να έχει το ίδιο δυναμικό (αγωγός) άλλά διαφορετικό από πριν.
Αυτό πως δικαιολογείται;

Απάντηση:

1) Γιατί να υπολογίσουμε το δυναμικό στην κάθετη στο κέντρο του δίσκου και όχι σε κάποιο άλλο σημείο;

Στο σχήμα φαίνεται το ηλεκτρικό πεδίο ενός ομοιόμορφα θετικά φορτισμένου δίσκου. Το πεδίο μπορεί να θεωρηθεί ομογενές σε μια περιοχή γύρω από το κέντρο του, αλλά διαφοροποιείται όταν κινούμαστε προς την περιφέρειά του.

Στο παρακάτω σχήμα βλέπουμε το πεδίο κατά μήκος μιας διαμέτρου του.

Στο σχήμα με διακεκομμένες γραμμές έχουν σχεδιαστεί οι ισοδυναμικές επιφάνειες του πεδίου (οι οποίες είναι κάθετες στις δυναμικές γραμμές). Προσέξτε ότι το δυναμικό παραμένει σταθερό σε μια μεγάλη περιοχή, όχι όμως προς τα άκρα του.

Αν κάπου πάνω από την πλάκα αυτή φέρουμε έναν αγωγό, τι δυναμικό θα αποκτήσει;

Στα παρακάτω σχήματα, φαίνεται το ηλεκτρικό πεδίο ενός σημειακού θετικού φορτίου (αριστερά) ενώ στα δεξιά του οι ισοδυναμικές επιφάνειες, αν σε ορισμένη απόσταση φέρουμε μια μεταλλική αφόρτιστη σφαίρα.

Η σφαίρα αποκτά δυναμικό, όσο ήταν το δυναμικό αρχικά, στο σημείο Α, όπου τώρα έχουμε τοποθετήσει το κέντρο της.

Δείτε αναλυτικά το τι συμβαίνει από:

Α) SERWAY , Τόμος ii. Σελ. 69.

Β) BERKELEY , Τόμος 2, σελ. 98.

Ας έρθουμε λοιπόν τώρα στον επίπεδο πυκνωτή.

i) Υπολογίζουμε το δυναμικό στην κάθετη στο κέντρο του δίσκου, αφού τόσο είναι ΣΧΕΔΟΝ και το δυναμικό σε όλη την έκταση και μας είναι πιο εύκολος ο υπολογισμός του δυναμικού.

ii) Όταν φέρουμε τον άλλο οπλισμό σε απόσταση ℓ, δεν αλλάζει ουσιαστικά το δυναμικό που οφείλεται στον πρώτο οπλισμό.

2) Για να δούμε όμως επ’ ευκαιρία τι ακριβώς κάνουμε με τα μαθηματικά; Υπολογίζουμε με ακρίβεια τα μεγέθη που θέλουμε πάντα;

Όταν π.χ. υπολογίζουμε την χωρητικότητα του πυκνωτή C=ε₀∙s/ℓ, είναι σωστό το αποτέλεσμα; Μα αυτός ο τύπος προέκυψε από εφαρμογή του νόμου του Gauss, θεωρώντας άπειρη την φορτισμένη επιφάνεια και ότι το ηλεκτρικό πεδίο περιορίζεται αυστηρά στο εσωτερικό του πυκνωτή.

Πάρτε για παράδειγμα ένα σωληνοειδές. Η ένταση του Μ.Π, που δίνει η εξίσωση Β=μ₀in, πότε και για ποια σημεία ισχύει; Βλέπετε κάποια αναλογία;

Ένας κυκλικός αγωγός ακτίνας R διαρρέεται από ρεύμα Ι. Μπορούμε να υπολογίσουμε τη μαγνητική ροή που διέρχεται από την επιφάνεια του αγωγού;

Γενικά μπορεί να υποστηριχθεί ότι η μαθηματική επεξεργασία ενός προβλήματος, γίνεται σε μερικές πολύ απλές περιπτώσεις και αφού δεχτούμε και ένα σωρό υποθέσεις, για να μπορούμε να πάρουμε αποτελέσματα. Η Φυσική πραγματικότητα, είναι ΠΑΝΤΑ πολύ πολύπλοκη για να προκύπτει από μια απλή λύση κάποιας μαθηματικής εξίσωσης.

Γιατί χρησιμοποίησες οπλισμό σχήματος κυκλικού δίσκου; Μα γιατί μου είναι πιο εύκολο το ολοκλήρωμα, ενώ δεν αλλάζει το αποτέλεσμα. Εκτός και αν δεχτούμε ότι η χωρητικότητα εξαρτάται και από το ΣΧΗΜΑ των οπλισμών.

Ναι αλλά είναι ομοιόμορφη η κατανομή των φορτίων στους δύο οπλισμούς; Όχι, αφού κοντά στην περιφέρεια έχουμε μεγαλύτερη επιφανειακή πυκνότητα (θυμάμαι σαν χθες, τον δάσκαλό μου τον κ. Μαυρία, να μας μιλάει για τη δύναμη των ακίδων…) Αλλά αν πάρουμε αυτήν την ανισοκατανομή, δεν θα βγάλουμε ποτέ αποτέλεσμα.

Μα έτσι γίνονται λάθη. Γιατί υπάρχει ένα ακριβές αποτέλεσμα που μας δίνει μια μαθηματική σχέση; Όχι συνάδελφοι. Μπορούμε με την βοήθεια των μαθηματικών να βγάζουμε εξισώσεις τέλειες, οι οποίες πάντα όμως έχουν προκύψει, αφού προηγούμενα έχουμε κάνει ένα σωρό απλοποιήσεις.

Και τότε γιατί τόσος κόπος για κάτι που δεν είναι και πολύ ακριβές;

Ας έρθουμε στο αποτέλεσμα της ανάρτησης Ενέργεια πυκνωτή.

Υπολογίσαμε την ενέργεια που απαιτείται για να απομακρύνουμε τους οπλισμούς ώστε να διπλασιάσουμε την απόσταση μεταξύ τους.

«Διπλασιάζοντας την απόσταση των οπλισμών, η χωρητικότητα υποδιπλασιάζεται αφού C=ε₀∙S/ℓ, ενώ το φορτίο παραμένει σταθερό, οπότε εφαρμόζοντας την αρχή διατήρησης της ενέργειας παίρνουμε:

U_αρχ + ΔΕ=U_τελ →

ΔΕ= U_τελ-U_αρχ = ½ q²/C₂- ½ q²/C₁= ½ q²/C₁ =U_αρχ. (2)»

Είναι σωστό αποτέλεσμα; Ναι είναι σωστό. Στηρίζεται στην αρχή διατήρησης της ενέργειας, δεν μπορεί να είναι λάθος.

Ωραία. Είσαστε σίγουροι ότι αν έχετε δύο παράλληλες μεταλλικές πλάκες σε απόσταση ℓ, τόση είναι η χωρητικότητα; Προφανώς όχι ακριβώς…

Στην απόδειξη βγάλαμε:

η οποία αν λάβουμε υπόψη τις προσεγγίσεις R²+ℓ² ≈R² και R²+4ℓ² ≈R² καταλήγουμε ότι:

W_Fεξ= ½ q²/C. (2)

Είναι σωστό το αποτέλεσμα; Θα έλεγα ότι ναι είναι σωστό, χωρίς να σημαίνει ότι δεν περιέχει κανένα σφάλμα. Περιέχεται σφάλμα και εδώ, όπως περιέχεται και στο προηγούμενο με την χωρητικότητα.

Έτσι επανερχόμαστε στο βασικό ερώτημα. Γιατί αυτή η απόδειξη; Τι στόχους είχε;

Ας τους ορίσουμε λοιπόν.

Ποια ενέργεια ονομάζουμε ενέργεια πυκνωτή; Είναι θετική ή αρνητική; Γιατί απαιτείται να προσφέρουμε ενέργεια τραβώντας τον έναν οπλισμό του πυκνωτή, ώστε να αυξήσουμε την απόστασή τους; Μπορούμε να εφαρμόζουμε τον τρόπο που δείχνει η εξίσωση (2) για να υπολογίσουμε την απαιτούμενη ενέργεια και αν ναι, μέχρι ποια απόσταση; Μέχρι και την πλήρη απομάκρυνση; Και αν η απόσταση γίνει άπειρη, η ενέργεια που θα απαιτηθεί θα είναι άπειρη;

Ο τρόπος της μελέτης απάντησε νομίζω στα παραπάνω ερωτήματα και δεν έχει καμιά αξία αν η απαιτούμενη ενέργεια είναι ίση με:

W_Fεξ= U_αρχ∙R/ℓ ή είναι W_Fεξ= 1,05∙U_αρχ∙R/ℓ ή είναι W_Fεξ= 0,95∙ U_αρχ∙R/ℓ.